Number sense
Number sense
Number sense
Number sense is considered as an innate numeracy skill, which not only humans but also some animals, such as fish and birds have. As the name says, it refers to sense of numbers. Number sense enables us to estimate the number of cars on the parking lot without counting them on-by-one, or to tell whether there are more people queueing in one line or in the other one.
APPROXIMATE NUMBER SYSTEM (ANS)
It has been proposed that we use a system called approximate number system, ANS, when estimating magnitudes (e.g. object or dots) approximately, or making comparisons of numbers (1).
When testing what kind of number sense an individual has, researchers often use tasks, in which you need to compare a number of dots or number symbols. Those who have a good number sense often respond quicker and more accurately in these tasks compared to those with weaker number sense.
Look at the pictures.
Can you quickly estimate which of the pictures has more dots?
Number sense is considered as an innate numeracy skill, which not only humans but also some animals, such as fish and birds have. As the name says, it refers to sense of numbers. Number sense enables us to estimate the number of cars on the parking lot without counting them on-by-one, or to tell whether there are more people queueing in one line or in the other one.
APPROXIMATE NUMBER SYSTEM (ANS)
It has been proposed that we use a system called approximate number system, ANS, when estimating magnitudes (e.g. object or dots) approximately, or making comparisons of numbers (1).
When testing what kind of number sense an individual has, researchers often use tasks, in which you need to compare a number of dots or number symbols. Those who have a good number sense often respond quicker and more accurately in these tasks compared to those with weaker number sense.
Look at the pictures.
Can you quickly estimate which of the pictures has more dots?
Number sense is considered as an innate numeracy skill, which not only humans but also some animals, such as fish and birds have. As the name says, it refers to sense of numbers. Number sense enables us to estimate the number of cars on the parking lot without counting them on-by-one, or to tell whether there are more people queueing in one line or in the other one.
APPROXIMATE NUMBER SYSTEM (ANS)
It has been proposed that we use a system called approximate number system, ANS, when estimating magnitudes (e.g. object or dots) approximately, or making comparisons of numbers (1).
When testing what kind of number sense an individual has, researchers often use tasks, in which you need to compare a number of dots or number symbols. Those who have a good number sense often respond quicker and more accurately in these tasks compared to those with weaker number sense.
Look at the pictures.
Can you quickly estimate which of the pictures has more dots?
Arithmetic skills
Arithmetics include four operations, namely addition, subtraction, multiplication and division. Children start practicing and learning addition and subtraction skills already before they start schooling, first with concrete objects, and later on they can retrieve simple addition and subtraction facts (e.g., 3 + 4 = 7 or 12 - 6 = 6) from memory. After getting familiar with basic addition and subtraction (within the number range 1–20), children start learning multiplication and division.
CALCULATION STRATEGIES
Children use different calculation strategies while solving arithmetic problems. These strategies also reflect the stage in their development of arithmetic skills.
In the beginning, it is common that children use concrete objects (e.g., fingers, cubes, buttons) as their memory aids while solving a problem (1). In an addition task, for example 2 + 4, they first count each addend "one, two" and "one, two, three, four" and then the total together "one, two, three, four, five, six". A more advanced strategy is to start counting on from the first addend "two....three, four, five, six" and later on to start from the bigger number, as then there are less steps to count, "four...five, six".

Gradually, by practicing and getting enough correct answers, there starts to build up a connection between the problem (e.g., 4 + 5) and the answer (9), and the child is able to remember, to retrieve, the answer to the problem fast from memory. Being able to retrieve answers for simple arithmetic problems is an important skill for later mathematics learning. When solving a more challenging arithmetic problem, for example doing word problem solving tasks with multi-digit numbers, the child can then focus on solving other parts in that problem than using much time and energy for simple calculations.
While learning more complex arithmetic facts, such as going over ten (8 + 9), a child may use as a help some already learned facts (2). Often the children learn pretty early so called doubles facts (e.g., 2 + 2, 3 + 3, 4 + 4) . For example, when solving a problem 8 + 9, the child may recall that 8 + 8 = 16. As knowing that 9 is one more than 8, the child then only adds one more to this double fact, (8 + 8) + 1 = 17. When teaching children how to take advantage of already known facts, it is good to take care of that the children also understand how different strategies work, using for example math manipulatives (e.g., cubes).
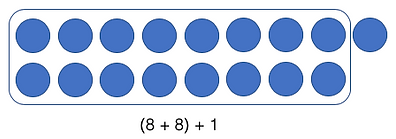
In general, children use different strategies flexibly, according to the problem they have to solve (2). Those children, who have mathematical learning difficulties, often struggle with learning basic arithmetic facts and retrieving them from memory. Compared to their age peers, they use more immature strategies, such as their fingers as memory aids and counting-based strategies. Research has shown that teaching children systematically more efficient calculation strategies, is beneficial (3).
IN OUR PROJECT
In our project children's addition, subtraction and multiplication fluency is assessed. In addition, children's arithmetic skills are assessed in word problems solving tasks.
REFERENCES
(1) Fuson, K. C. (1992). Research on whole number addition and subtraction. In D. A. Grouws (Ed.) Handbook of Research on Mathematics Teaching and Learning, (pp. 243–275). Reston, VI: NCTM.
(2) Sarama, J., & Clements, D. H. (2009). Early childhood mathematics education research. Learning trajectories for young children. New York, NY: Routledge.
(3) Koponen, T., Sorvo, R., Dowker, A., Räikkönen, E., Viholainen, H., Aro, T., & Aro, M. (2018). Does multi-component strategy training improve calculation fluency among poor performing elementary school children? Frontiers in Psychology, 9 (1187).
Written by Riikka Mononen (2019)